I’ve been learning a bit about bit operations and bitmasks, and wanted to try applying them to a musical concept - building an interactive piano. Let’s see how it goes!
Contents
Using an array
When working on an interactive piano, one of the first questions/challenges is how to store the current state of the piano - i.e., how do we know which keys are being played right now? We need to store this state in an organized, comprehensive way in our application, so that we can easily react when the user interacts with the piano.
Let’s consider just one octave of a piano for now, to keep things simple. On a piano, one octave is comprised of 12 keys, representing the 12 notes of a scale in Western music (we see 13 keys here because we also have the C in the next octave):
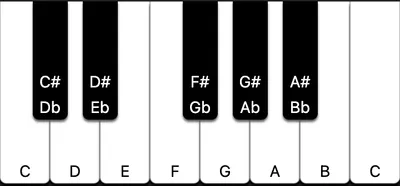
In my past projects, I’ve stored the state of the keys as an array of booleans. Each piano key is assigned an index in the array: 0 is C, 1 is C#/Db, 2 is D, and so on. Then, each value represents whether the key is currently being played - either true or false. For example, if the notes C and D are currently being played at the same time, the state would look like this:
/** State array - C and D are being played */const state = [true, false, true, false, false, ...];Storing the state as an array allows for easy access to the state of each piano key. For each key, we can just check the corresponding index on the array to see if the key is being played, and then react accordingly in our application (change the key’s color, play sound, etc.)
But, I’m not convinced that an array is the best way to store the piano’s state. An array takes up space in memory for every element, and for a full-size piano, we’d need to store the state of 88 keys. On top of that, in most JavaScript frameworks, if you’re storing state as an array, that array needs to be re-created in memory each time the state changes. So, every time you play or release a key, we need to re-create the whole array, which seems a bit wasteful. Is there a more compact, efficient way we could represent the state of the piano keys, that mirrors how computers operate at a low level?
Bit fields, masks, and operations
Bits
At the very low level of computers, data is stored and manipulated as bits, just 1s and 0s. We can think of each bit as a light switch, that we can turn ‘on’ (1) and ‘off’ (0).
With bits, integers can be stored in their binary (base 2) representation. Here’s the human number 5, translated to it’s binary representation in a computer’s memory. This is interactive, so you can click to toggle the bits between 0 and 1 in the table, and see how that translates to our human (base 10) number:
Base 10 number: 5
Base 2 (binary): 00000101
(Technically in JavaScript, there’s something a little more complicated going on under the hood, since numbers in JS can be decimals, not just integers, and they use 64 bits. But we’ll keep things simple here 😅)
Bit fields and masks
A series of bits doesn’t have to just represent a number, though. We could take a bunch of bits (sometimes called a bit field, or bit set) and then give each individual bit a special meaning - say, a note in a musical scale! So, let’s expand out to 13 bits to represent one octave of piano keys, and then assign each note to a specific bit in our bit field:
| Note | Base 2 (bitmask) | Base 10 || ----- | ---------------- | ------- || C | 1000000000000 | 4096 || C#/Db | 0100000000000 | 2048 || D | 0010000000000 | 1024 || D#/Eb | 0001000000000 | 512 || E | 0000100000000 | 256 || F | 0000010000000 | 128 || F#/Gb | 0000001000000 | 64 || G | 0000000100000 | 32 || G#/Ab | 0000000010000 | 16 || A | 0000000001000 | 8 || A#/Bb | 0000000000100 | 4 || B | 0000000000010 | 2 |Notice that each note is associated with a specific bit (the position of the 1) in the bit field, and that in turn translates into a unique numeric value. This unique value associated with each note is called a bitmask. Typically in applications, bitmasks are used as an efficient way to represent various settings or flags.
Now that each note has a bitmask, we can use this to toggle notes on and off in a bit field. But how do we do that exactly? Well, we’ll need to learn some bit math, also known as bitwise operations. (are you ready??)
Bit operations
We’ll start with the initial state of the piano - no keys are being played, which will be represented by 13 zeros (you can think of 13 light switches in a row, all turned ‘off’):
initial state: 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | CBitwise OR
Now, let’s say the user plays a D. We want to flip the third bit from a zero (off) to a one (on). To do this, we’ll grab the bitmask of D from the table above, and then apply it to the initial state using the OR (|) operator:
initial state: 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 OR (|) bitmask of D: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 EQUALS (=) new state: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)What does this OR operator do exactly? It takes two binary values, and if a 1 is found in any position in either value, the resulting value will have a 1 in that position. So by taking our initial state, and the bitmask of the note D, the OR operator forces the corresponding bit to be a 1 (‘on’).
Now let’s say the user plays A, without letting go of D. We’ll take the bitmask of A and apply it to the current state of the piano, again using the OR operator:
current state: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 OR (|) bitmask of A: 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 EQUALS (=) new state: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)Now, both D and A are set to the 1 / ‘on’ state. Notice that by using the bitmask and the OR operation, it doesn’t affect any other bits in the state - it only acts on the bit that we want.
Bitwise AND
How does our application check whether a certain note is currently being played? We’ll need another operator - the AND operator. The AND operator (&) takes two binary values, and if a 1 is found in the same position in both values, it will return a 1 in the same position in the resulting value. Otherwise, it returns a 0.
Let’s say the user is still holding down the D and A, and now our application needs to check whether D is still being played. So, we take our current state, along with the bitmask of the note we’re wondering about, and do an AND operation.
current state: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 AND (&) bitmask of D: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 EQUALS (=) result: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)Since the resulting value has a 1, we know that the note D is currently being played. Simple! (have I lost you yet?)
Bitwise NOT
Ok, we have a way to toggle notes ‘on’, and we have a way to check if any note is being played. But we still need a way to toggle notes ‘off’! We’ll need to do something a little more involved here.
Our user is still holding the D and A keys. Now, they let go of A. First, we’ll do a NOT operation on the bitmask of A. The NOT operator (~), unlike the others we’ve seen, only operates on a single value. It will just flip every bit: 0s become 1s, and 1s become 0s:
NOT (~) bitmask of A: 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 EQUALS (=) result: 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)We’ll take this ‘flipped’ bitmask of the A key, and then do an AND operation with the current state of the piano. Watch what happens:
current state: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 AND (&)NOT bitmask of A: 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 EQUALS (=) result: 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)Remember that the AND operation will return a 1 only if both values have a 1 in the same position. By combining the AND and NOT operators, we force the A key into the zero / ‘off’ position, without affecting any other keys.
Bit shifts
By using bits to represent keys of the piano, we can also recognize some interesting patterns in the keys being currently played. For example, we can see the intervals between notes by looking at the patterns of 1s and 0s.
In music theory, we call the distance from one piano key to the very next key a half step. Two half steps will make a whole step. Here is what whole steps would look like in our bit field. Notice any patterns?
C and D: 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 F and G: 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 A and B: 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 (notes: C | C#| D | D#| E | F | F#| G | G#| A | A#| B | C)A whole step will always have the pattern of 101 in our bit field, although it can appear in different positions. We could use patterns like this one to detect whether a user is playing a certain interval or chord!
To detect these patterns easily in our code, we’ll first need to get rid of all those zeros on the right. We can do this by using a bit shift operator (>>). Let’s take F and G as an example:
F and G: 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 SHIFT RIGHT (>>) 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 SHIFT RIGHT (>>) 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 repeat until... 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1We shift all the bits to the right until we see a 1 at the rightmost position. Once we have that, we can compare the result to certain patterns (101 for a whole step, 11 for a half step), to see if the user is playing a specific interval or chord.
Summary of bitwise operations
- To a toggle a note on, we take the current state of the piano and the note’s bitmask, and do an OR operation.
- To check if a note is being played, we take the current state of the piano and the note’s bitmask, and do an AND operation. If there’s a 1 in the result, the note is being played.
- To toggle a note off, we take the NOT of the note’s bitmask, and then do an AND operation with the current state of the piano.
- To detect common intervals or chords in the notes being played, we shift (>>) the bits to the right until there’s a 1 in the rightmost position.
Interactive Demo
Alright, enough talk. Here’s a demo of a one-octave piano, represented by a bit field! There’s no sound here - this is purely for visualization purposes to see how the state changes as we interact with the keys. You can click on the piano keys, and you can also click on the individual bits in the table to toggle them on and off. Notice how each combination of keys has a unique state value associated with it, and how we can identify patterns and intervals from the bits.
Code
I’m using the Svelte framework here, as it allows for some easy state management and reactivity. (I’ve left out the CSS below, since that’s not the interesting part)
<script lang="ts"> /** * Constant array of metadata for 12 piano keys (one octave). Each piano key is given a * unique bitmask value that's a power of 2, starting with 4096 (2 ^ 12) and descending. * * For example: `[ { name: "C", value: 4096 }, { name: "C# Db", value: 2048 }, ... ]` */ const KEYS = Object.freeze( ["C", "C# Db", "D", "D# Eb", "E", "F", "F# Gb", "G", "G# Ab", "A", "A# Bb", "B", "C"].map( (name, idx) => ({ name, value: 2 ** (12 - idx) }), ), ); const KEY_INDEXES = Object.freeze([...KEYS.keys()]); const BLACK_KEY_INDEXES = Object.freeze([1, 3, 6, 8, 10]);
/** The "bit field" integer that represents the state of all keys */ let state = $state(0); const stateBinary = $derived(state.toString(2).padStart(13, "0"));
/** Event handlers */ function onKeyDown(keyIndex: number) { state = state | KEYS[keyIndex].value; // OR (|) operator will set this key's bit to 1 } function onKeyUp(keyIndex: number) { state = state & ~KEYS[keyIndex].value; // AND (&) and NOT (~) operators will set this key's bit to 0 } function onKeyToggle(keyIndex: number) { state = state ^ KEYS[keyIndex].value; // XOR (^) operator will toggle this key's bit between 0 and 1 }
/** Interval/chord detector */ const { isHalfStep, isWholeStep, isPerfectFifth, isMajorTriad, isMinorTriad } = $derived.by( () => { let shiftedState = state; // shift all bits to the right until we get a 1 while (shiftedState !== 0 && (shiftedState & 1) === 0) { shiftedState >>= 1; } // check the shifted bits for patterns that indicate certain intervals & chords return { isHalfStep: shiftedState === 0b11, isWholeStep: shiftedState === 0b101, isPerfectFifth: shiftedState === 0b10000001, isMajorTriad: shiftedState === 0b10001001, isMinorTriad: shiftedState === 0b10010001, }; }, );</script>
<div class="wrapper"> <div class="keyboard"> <div> {#each KEY_INDEXES as keyIndex (keyIndex)} <!-- AND (&) operator to check if key is played --> {@const isKeyPlayed = state & KEYS[keyIndex].value} <button onclick={() => (isKeyPlayed ? onKeyUp(keyIndex) : onKeyDown(keyIndex))} class="key" class:played={isKeyPlayed} class:black={BLACK_KEY_INDEXES.includes(keyIndex)} class:white={!BLACK_KEY_INDEXES.includes(keyIndex)} > <span class="key-label">{KEYS[keyIndex].name}</span> </button> {/each} </div> </div> <div class="bits"> <b>Note</b> {#each KEY_INDEXES as idx} <div>{KEYS[idx].name}</div> {/each} <b>Bit</b> {#each [...stateBinary] as bit, idx} <button class:selected={+bit === 1} onclick={() => onKeyToggle(idx)}> {bit} </button> {/each} </div> <div>Binary state (base 2): {stateBinary}</div> <div>Integer state (base 10): {state}</div> <div>Half step: {isHalfStep ? "✅" : "❌"}</div> <div>Whole step: {isWholeStep ? "✅" : "❌"}</div> <div>Perfect fifth: {isPerfectFifth ? "✅" : "❌"}</div> <div>Major triad: {isMajorTriad ? "✅" : "❌"}</div> <div>Minor triad: {isMinorTriad ? "✅" : "❌"}</div></div>Drawbacks
Now, is a bit field the most sensible way to hold the state of the piano in an actual application? Probably not 😅, and here are a few reasons why:
- It makes debugging quite tricky. Imagine if there’s a bug somewhere in the app - now you have to dive into all the bit math just to figure out what’s going on.
- The performance gains of bit operations vs. just using an array might be quite modest in an interpreted scripting language like JavaScript. You know what they say about premature optimization…
- It’s not easily extensible. If you wanted to store additional information, like the volume/velocity of each key played, you’d need an additional piece of state. In that case, you might as well go with an array or hashmap, where we can add data as needed.
All that being said, is this a cool way to learn about and visualize bitwise operations, and even learn some music theory in the process? I would say yes!
